逐层分解Transformer

约 3570 字大约 12 分钟

2025-07-07

1. 1.Transformer 整体结构

首先介绍 Transformer 的整体结构，下图是 Transformer 用于中英文翻译的整体结构：

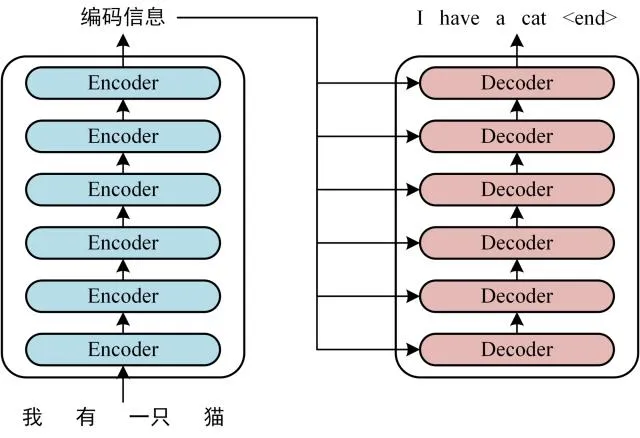
Transformer 的整体结构，左图Encoder和右图Decoder

可以看到 Transformer 由Encoder 和Decoder两个部分组成，Encoder 和Decoder 都包含 6 个 block。

Transformer 的工作流程大体如下：
- 第一步：获取输入句子的每一个单词的表示向量 X，X由单词的 Embedding（Embedding就是从原始数据提取出来的Feature）和单词位置的 Embedding 相加得到。

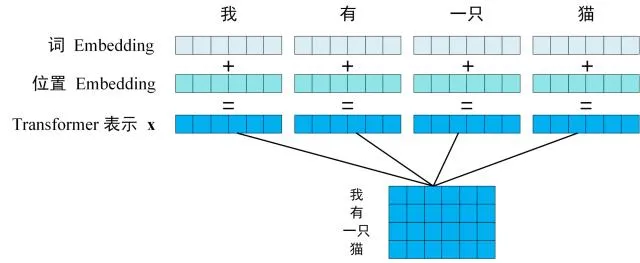
Transformer 的输入表示

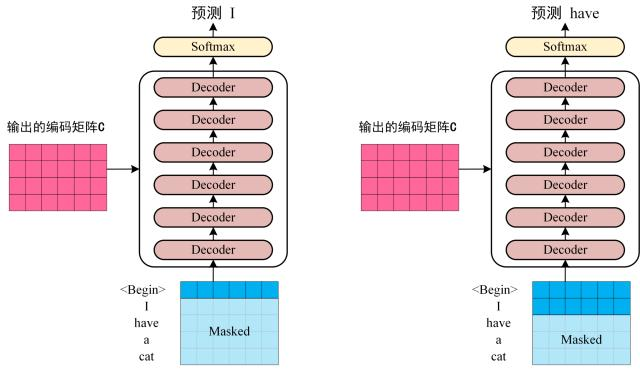
Transofrmer Decoder 预测

上图Decoder接收了 Encoder 的编码矩阵 C，然后首先输入一个翻译开始符 "<Begin>"，预测第一个单词 "I"；然后输入翻译开始符"<Begin>" 和单词 "I"，预测单词 "have"，以此类推。这是 Transformer 使用时候的大致流程，接下来是里面各个部分的细节。

2. Transformer 的输入

Transformer 中单词的输入表示 x由单词 Embedding 和位置 Embedding （Positional Encoding）相加得到。

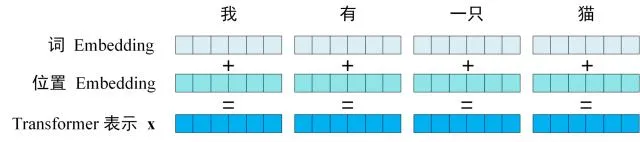
Transformer 的输入表示

2.1 单词 `Embedding`

单词的 Embedding有很多种方式可以获取，例如可以采用 Word2Vec、Glove 等算法预训练得到，也可以在 Transformer 中训练得到。

Transformer 中除了单词的 Embedding，还需要使用位置 Embedding 表示单词出现在句子中的位置。因为 Transformer 不采用 RNN 的结构，而是使用全局信息，不能利用单词的顺序信息，而这部分信息对于 NLP 来说非常重要。所以 Transformer 中使用位置 Embedding 保存单词在序列中的相对或绝对位置。

位置 Embedding 用 PE表示，PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到，也可以使用某种公式计算得到。在 Transformer 中采用了后者

计算公式如下：

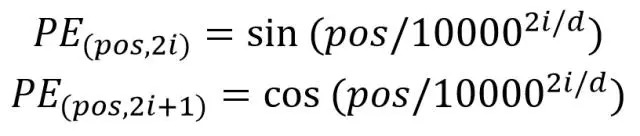
其中，pos 表示单词在句子中的位置，d 表示 PE的维度 (与词 Embedding 一样)，2i 表示偶数的维度，2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)。使用这种公式计算 PE 有以下的好处：

注

使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
可以让模型容易地计算出相对位置，对于固定长度的间距 k，PE(pos+k) 可以用 PE(pos) 计算得到。
因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。

3. Self-Attention（自注意力机制）

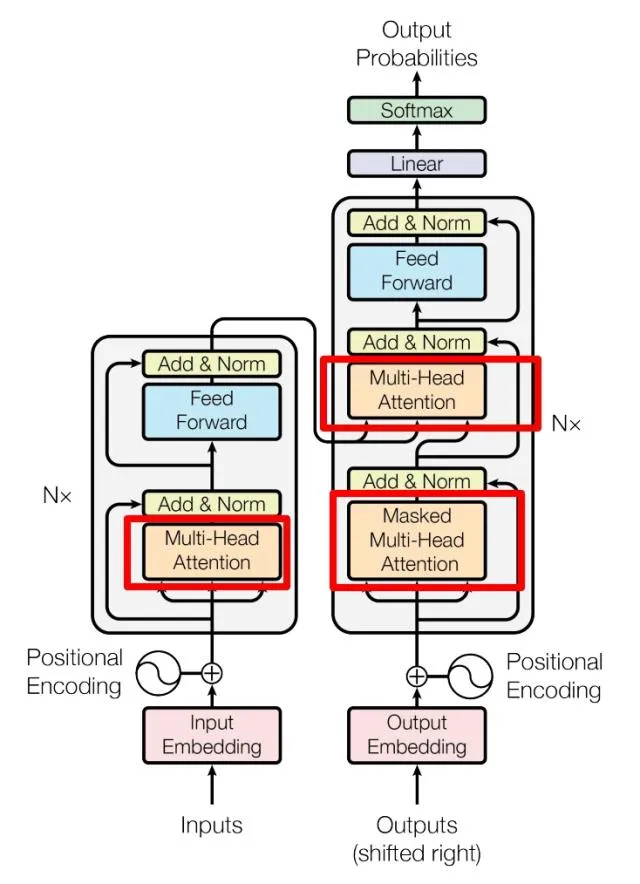
Transformer 的内部结构图

左侧为 Encoder block
右侧为 Decoder block
红色圈中的部分为 Multi-Head Attention，是由多个 Self-Attention组成的

可以看到 Encoder block 包含一个 Multi-Head Attention
而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。
Multi-Head Attention上方还包括一个 Add & Norm 层
Add 表示残差连接 (Residual Connection) 用于防止网络退化，
Norm 表示 Layer Normalization，用于对每一层的激活值进行归一化。

因为 Self-Attention是 Transformer 的重点，所以我们重点关注 Multi-Head Attention 以及 Self-Attention，首先详细了解一下 Self-Attention 的内部逻辑。

3.1 `Self-Attention 结构`

Self-Attention 结构

上图是 Self-Attention的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中，Self-Attention 接收的是输入(单词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的。

3.2 `Q, K, V 的计算`

Self-Attention的输入用矩阵X进行表示，则可以使用线性变阵矩阵WQ,WK,WV计算得到Q,K,V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。

Q, K, V 的计算

实现

# self-attention 实现
import numpy as np
from math import sqrt
import torch
from torch import nn


class Self_Attention(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self, input_dim, dim_k, dim_v):
        super(Self_Attention, self).__init__()
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)
        self._norm_fact = 1 / sqrt(dim_k)

    def forward(self, x):
        Q = self.q(x)  # Q: batch_size * seq_len * dim_k
        K = self.k(x)  # K: batch_size * seq_len * dim_k
        V = self.v(x)  # V: batch_size * seq_len * dim_v

        # Q * K.T() # batch_size * seq_len * seq_len
        atten = nn.Softmax(
            dim=-1)(torch.bmm(Q, K.permute(0, 2, 1))) * self._norm_fact

        # Q * K.T() * V # batch_size * seq_len * dim_v
        output = torch.bmm(atten, V)

        return output


X = torch.randn(4, 3, 2)
print(X)
self_atten = Self_Attention(2, 4, 5)  # input_dim:2, k_dim:4, v_dim:5
res = self_atten(X)
print(res.shape)  # [4,3,5]

3.3 `Self-Attention 的输出`

得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了，计算的公式如下：

Self-Attention 的输出

公式中计算矩阵Q和K每一行向量的内积，为了防止内积过大，因此除以 $$d_k$$的平方根。Q乘以K的转置后，得到的矩阵行列数都为 n，n 为句子单词数，这个矩阵可以表示单词之间的 attention 强度。下图为Q乘以$$K^{T}$$ ，1234 表示的是句子中的单词。

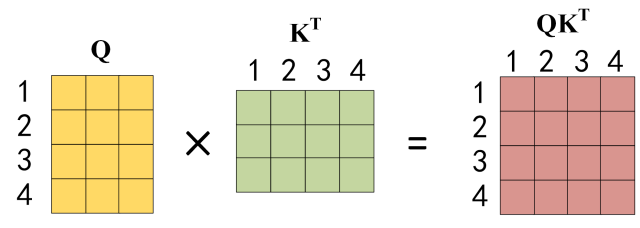
Q乘以K的转置的计算

得到$$QK^{T}$$之后，使用 Softmax 计算每一个单词对于其他单词的 attention 系数，公式中的 Softmax是对矩阵的每一行进行 Softmax，即每一行的和都变为 1.

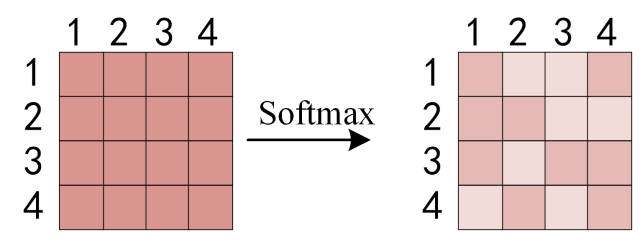
对矩阵的每一行进行 Softmax

得到 Softmax 矩阵之后可以和V相乘，得到最终的输出Z。

Self-Attention 输出

上图中Softmax矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数，最终单词 1 的输出 $$Z_1$$ 等于所有单词 i 的值 $$V_i$$ 根据 attention 系数的比例加在一起得到，如下图所示：

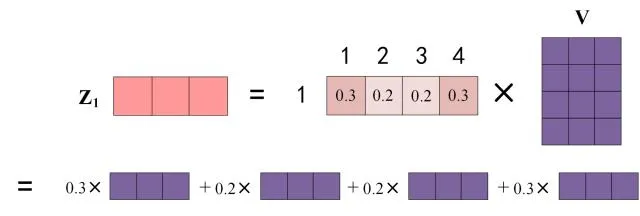
Zi 的计算方法

3.4 `Multi-Head Attention`

在上一步，我们已经知道怎么通过 Self-Attention计算得到输出矩阵 Z，而 Multi-Head Attention 是由多个 Self-Attention 组合形成的，下图是论文中 Multi-Head Attention 的结构图。

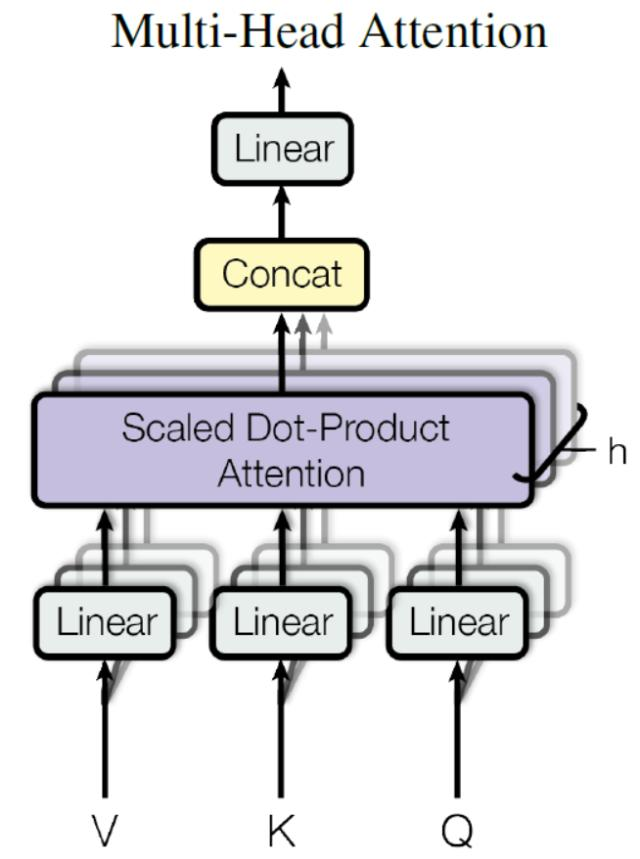
Multi-Head Attention

从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层，首先将输入X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵Z。下图是 h=8 时候的情况，此时会得到 8 个输出矩阵Z。

实现

#%%
# Muti-head Attention 机制的实现
from math import sqrt
import torch
import torch.nn as nn


class Self_Attention_Muti_Head(nn.Module):
    # input : batch_size * seq_len * input_dim
    # q : batch_size * input_dim * dim_k
    # k : batch_size * input_dim * dim_k
    # v : batch_size * input_dim * dim_v
    def __init__(self,input_dim,dim_k,dim_v,nums_head):
        super(Self_Attention_Muti_Head,self).__init__()
        assert dim_k % nums_head == 0
        assert dim_v % nums_head == 0
        self.q = nn.Linear(input_dim,dim_k)
        self.k = nn.Linear(input_dim,dim_k)
        self.v = nn.Linear(input_dim,dim_v)
        
        self.nums_head = nums_head
        self.dim_k = dim_k
        self.dim_v = dim_v
        self._norm_fact = 1 / sqrt(dim_k)
        
    
    def forward(self,x):
        Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head) 
        K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head) 
        V = self.v(x).reshape(-1,x.shape[0],x.shape[1],self.dim_v // self.nums_head)
        print(x.shape)
        print(Q.size())

        atten = nn.Softmax(dim=-1)(torch.matmul(Q,K.permute(0,1,3,2))) # Q * K.T() # batch_size * seq_len * seq_len
        
        output = torch.matmul(atten,V).reshape(x.shape[0],x.shape[1],-1) # Q * K.T() * V # batch_size * seq_len * dim_v
        
        return output
    
x=torch.rand(1,3,4)
print(x)
# %%
atten=Self_Attention_Muti_Head(4,4,4,2)
y=atten(x)
print(y.shape)

# %%

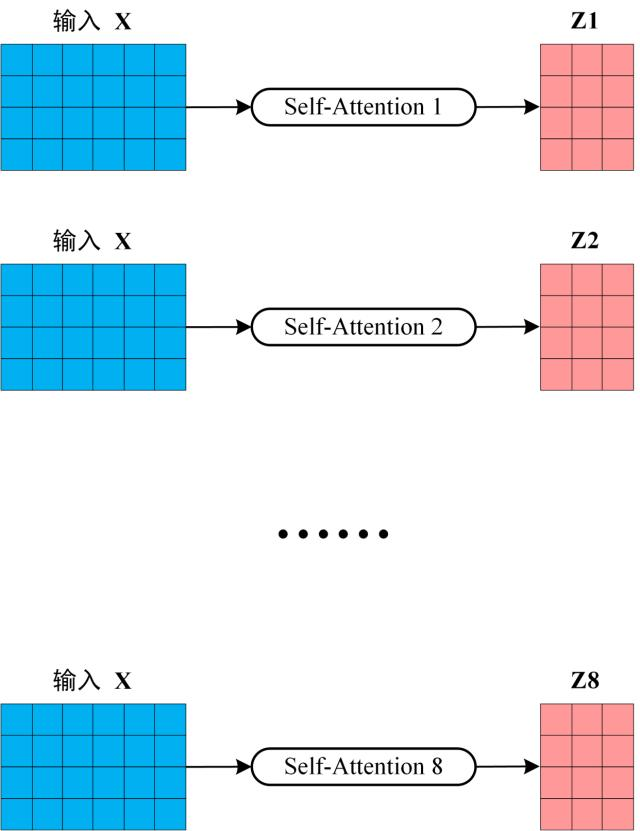
多个 Self-Attention

得到 8 个输出矩阵 $$Z_1$$ 到 $$Z_8$$之后，Multi-Head Attention将它们拼接在一起 (Concat)，然后传入一个Linear层，得到 Multi-Head Attention 最终的输出Z。

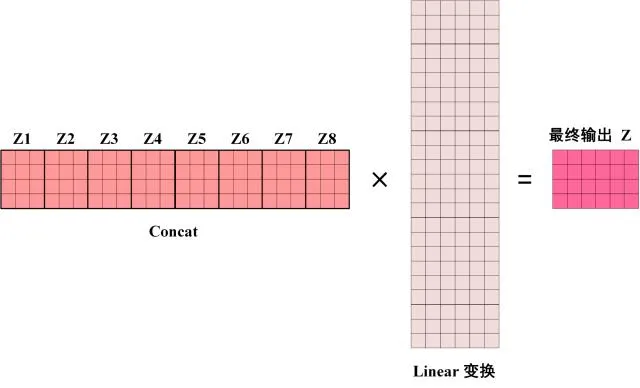
Multi-Head Attention 的输出

可以看到 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。

4. Encoder 结构

红色部分是 Transformer 的 Encoder block 结构，可以看到是由 Multi-Head Attention, Add & Norm, Feed Forward, Add & Norm 组成的。刚刚已经了解了 Multi-Head Attention 的计算过程，现在了解一下 Add & Norm 和 Feed Forward 部分。

Transformer Encoder block

4.1 Add & Norm

Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下：

Add &amp;amp;amp; Norm 公式

其中 X表示 Multi-Head Attention或者 Feed Forward 的输入，MultiHeadAttention(X) 和 FeedForward(X) 表示输出 (输出与输入 X 维度是一样的，所以可以相加)

Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到：

残差连接

Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。

4.2 Feed Forward

Feed Forward 层比较简单，是一个两层的全连接层，第一层的激活函数为 Relu，第二层不使用激活函数，对应的公式如下。

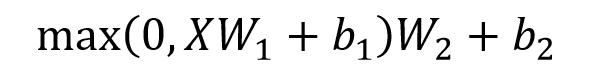
Feed Forward

X是输入，Feed Forward 最终得到的输出矩阵的维度与X一致。

4.3 组成 Encoder

通过上面描述的 Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block，Encoder block 接收输入矩阵 $$X_{(n\times d)}$$ ，并输出一个矩阵$$O_{(n\times d)}$$ 。通过多个 Encoder block 叠加就可以组成 Encoder。

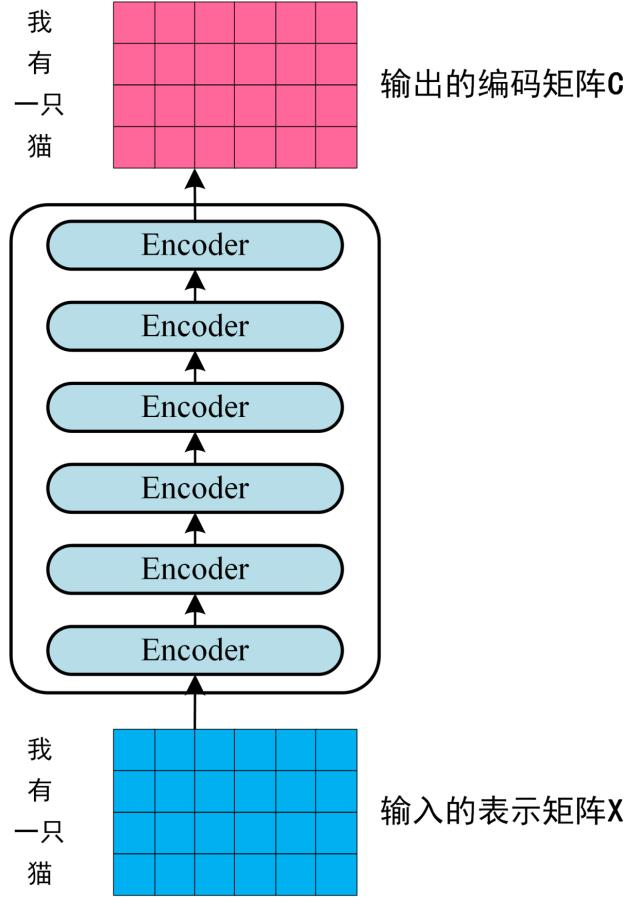
第一个 Encoder block 的输入为句子单词的表示向量矩阵，
后续Encoder block 的输入是前一个 Encoder block 的输出
最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后续会用到 Decoder 中。

5. Decoder 结构

红色部分为 Transformer 的 Decoder block 结构，与 Encoder block 相似，但是存在一些区别：

包含两个 Multi-Head Attention 层。
第一个 Multi-Head Attention 层采用了 Masked 操作。
第二个Multi-Head Attention 层的K, V矩阵使用 Encoder 的编码信息矩阵C进行计算，而Q使用上一个 Decoder block 的输出计算。
最后有一个 Softmax 层计算下一个翻译单词的概率。

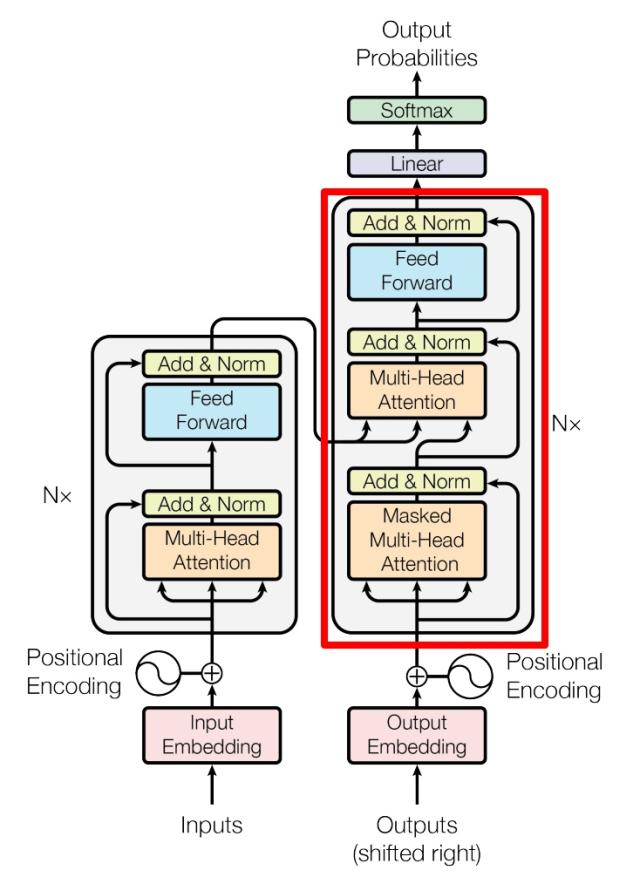
Transformer Decoder block

5.1 `第一个 Multi-Head Attention`

Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作，因为在翻译的过程中是顺序翻译的，即翻译完第 i 个单词，才可以翻译第 i+1 个单词。通过 Masked 操作可以防止第 i 个单词知道 i+1 个单词之后的信息。下面以 "我有一只猫" 翻译成 "I have a cat" 为例，了解一下 Masked 操作。

在 Decoder 的时候，是需要根据之前的翻译，求解当前最有可能的翻译，如下图所示。首先根据输入 "<Begin>" 预测出第一个单词为 "I"，然后根据输入 "<Begin> I" 预测下一个单词 "have"。

Decoder 预测

Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练，即将正确的单词序列 (<Begin> I have a cat) 和对应输出 (I have a cat <end>)传递到 Decoder。那么在预测第 i 个输出时，就要将第 i+1 之后的单词掩盖住，
注意 Mask 操作是在 Self-Attention 的 Softmax之前使用的，下面用 0 1 2 3 4 5 分别表示 <Begin> I have a cat <end>。

第一步：

1. 是 Decoder 的输入矩阵和 Mask 矩阵，输入矩阵包含 "<Begin> I have a cat" (0, 1, 2, 3, 4) 五个单词的表示向量，Mask 是一个 5×5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息，而单词 1 可以使用单词 0, 1 的信息，即只能使用之前的信息。

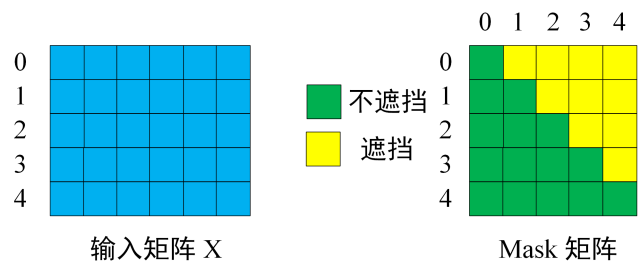
输入矩阵与 Mask 矩阵

第二步：

2. '接下来的操作和之前的 Self-Attention 一样，通过输入矩阵X计算得到Q,K,V矩阵。然后计算Q和 $$K^T\text{ 的乘积 }QK^T$$

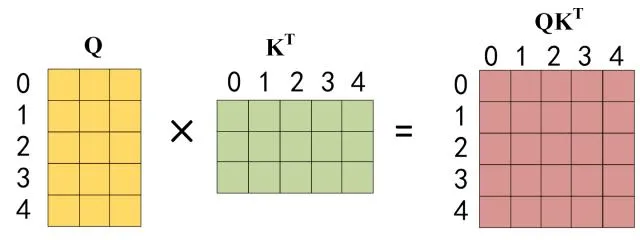
Q乘以K的转置

第三步：

3. 在得到 $$QK^{T}$$之后需要进行 Softmax，计算 attention score，我们在 Softmax 之前需要使用Mask矩阵遮挡住每一个单词之后的信息，遮挡操作如下：

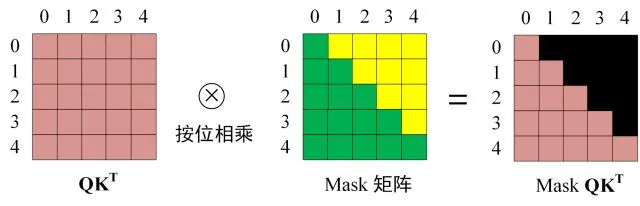
Softmax 之前 Mask

得到 Mask $$QK^{T}$$ 之后在 Mask $$QK^{T}$$上进行 Softmax，每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。

第四步：

4. 使用 Mask $$QK^{T}$$与矩阵 V相乘，得到输出 Z，则单词 1 的输出向量 $$Z_1$$ 是只包含单词 1 信息的。

第五步：

5. 通过上述步骤就可以得到一个 Mask Self-Attention 的输出矩阵 $$Z_i$$ ，然后和 Encoder 类似，通过 Multi-Head Attention 拼接多个输出$$Z_i$$ 然后计算得到第一个 Multi-Head Attention 的输出Z，Z与输入X维度一样。

5.2 `第二个 Multi-Head Attention`

Decoder block 第二个 Multi-Head Attention 变化不大，主要的区别在于其中 Self-Attention 的 K, V矩阵不是使用上一个Decoder block 的输出计算的，而是使用 Encoder 的编码信息矩阵 C 计算的。
根据 Encoder 的输出 C计算得到 K, V，根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个Decoder block则使用输入矩阵 X 进行计算)，后续的计算方法与之前描述的一致。
这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

5.3 `Softmax`预测输出单词

Decoder block 最后的部分是利用 Softmax 预测下一个单词，在之前的网络层我们可以得到一个最终的输出 Z，因为 Mask 的存在，使得单词 0的输出 Z0 只包含单词 0的信息，如下：

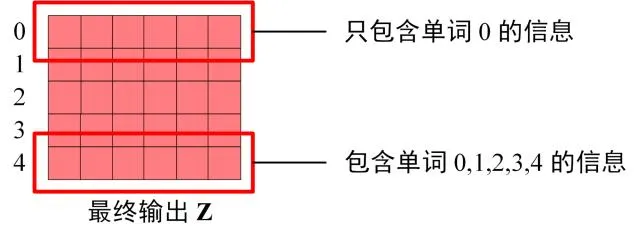
Decoder Softmax 之前的 Z

Softmax 根据输出矩阵的每一行预测下一个单词：

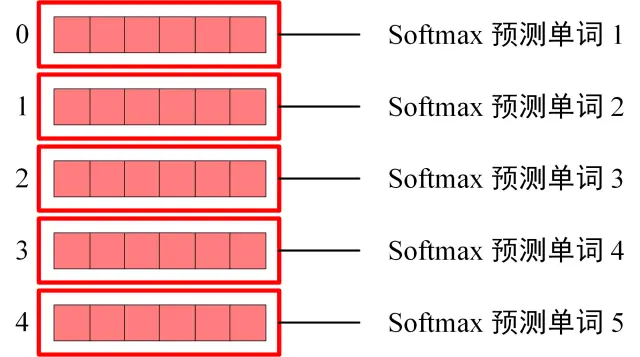
Decoder Softmax 预测

这就是 Decoder block 的定义，与Encoder一样，Decoder 是由多个 Decoder block 组合而成。

6. Transformer 总结

提示

Transformer 与 RNN 不同，可以比较好地并行训练。
Transformer 本身是不能利用单词的顺序信息的，因此需要在输入中添加位置 Embedding，否则 Transformer 就是一个词袋模型了。
Transformer 的重点是 Self-Attention 结构，其中用到的 Q, K, V矩阵通过输出进行线性变换得到。
Transformer 中 Multi-Head Attention 中有多个 Self-Attention，可以捕获单词之间多种维度上的相关系数 attention score。

贡献者

sreio

更新日志

2025/7/7 01:58

查看所有更新日志

61046-ai & sites于 2025/7/7